Estimating the Linear and Angular Velocities of an Object in Free Flight
Translation: Turkish
Estimation of an object's pose and motion while in free flight can a daunting task. Accuracy is difficult to obtain when working with limited camera hardware, wide-angle lenses, and severe effects of aerodynamics. Previous work has not seriously investigated vision-based estimation of angular information under the "full" effects of rigid body dynamics. Since highly accurate state estimation is not required in many robotics tasks, forces of drag and Magnus, or camera lens distortion, are often ignored.
In this work, the full state of a rigid body in free flight is tracked, including its position, rotation, velocity, and angular velocity. An extended Kalman Filter (EKF) is used with system dynamics involving forces of gravity, drag, and Magnus, and a camera model accounting for radial and tangential distortions.
System Dynamics and Imaging Model
The flying object is governed by the following system with a state vector s consisting of position p, rotation r (as a unit quaternion), velocity v, and angular velocity ω. The system dynamics are described by the nonlinear differential equation below. The velocity derivative includes forces of drag and Magnus along with their respective scalar coefficients ed and em. The matrix Q denotes the object's angular inertia matrix.
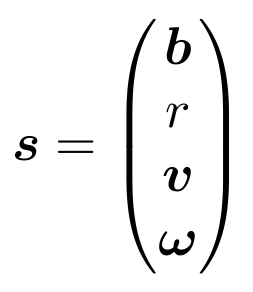
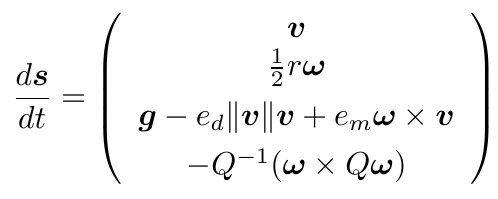
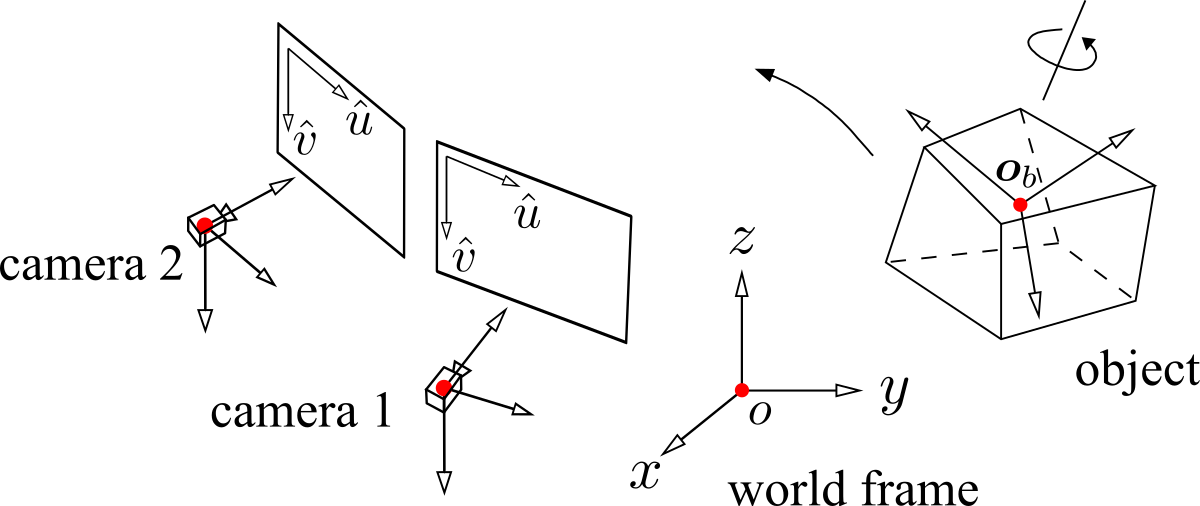
Two cameras in stereo vision observe the object throughout its flight. For a point on the object, the imaging model consists of transforming the point relative to a camera's coordinate system, applying distortion along the radial and tangential directions, and projecting the point onto the image plane. An iterative calibration procedure is used to obtain necessary camera parameters, including the its poses relative to a world frame.
State Estimation
An EKF is used to observe the object's state by evaluating the system dynamics in continuous time, while obtaining observables from the cameras at discrete time instants. Three incident edges on the object are extracted from images. Observables are obtained from the vertex shared by the three edges along with the phase angles of the three edge directions (shown below by dashed black lines). With known positions of vertices in the body frame, four points on the object can be distorted and projected into the image to obtain the estimated triple of edges (solid white lines).


Simulation with Various Objects
of a rod, pin, and bowl were simulated according to the dynamics model. The EKF was initialized with no knowledge of the object's state, and measurement errors were added to the observables. The table below shows errors after 200 iterations of the EKF.

Experiments with Accelerometers and a Stepper Motor
Four accelerometers were attached to a wooden frame object to transmit acceleration readings wirelessly while in flight. Given twelve readings, the linear and angular accelerations of the object can be computed from kinematics, followed by integration to obtain velocities. This data served as a ground truth to compare with the estimated velocities. Plotted below are the estimated (dashed lines) and observed (solid lines in lighter color) velocities.
 Angular Velocity
Angular Velocity
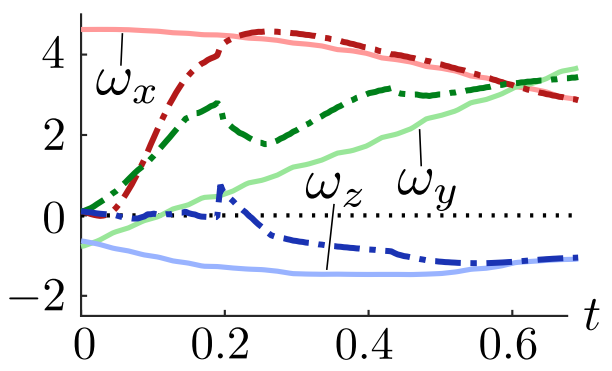
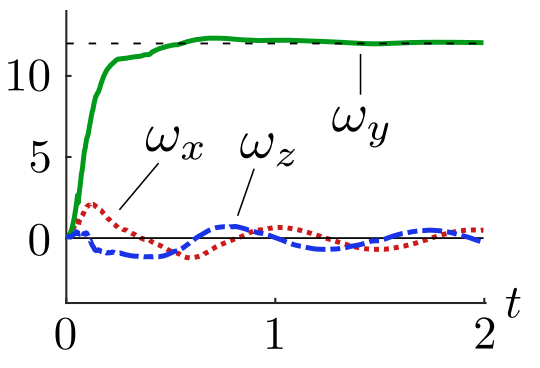
In addition, a cuboid object was attached to a stepper motor and configured to spin at 12 rad/s. The estimated angular velocity was again compared, where linear velocity was set to zero.
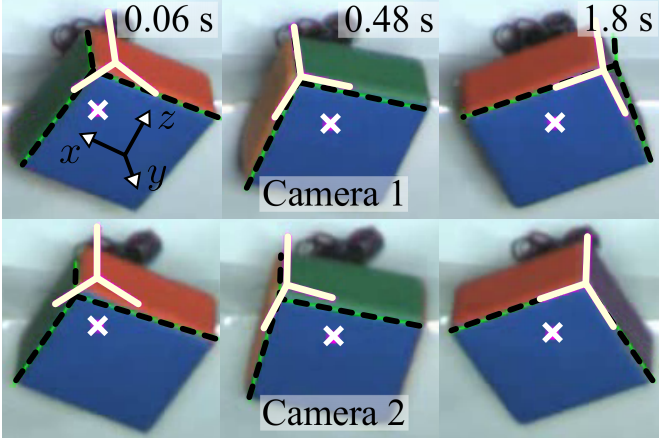 Angular Velocity
Angular Velocity
Results from these experiments and more can be seen in the YouTube video at the top of the page (link).
For more information, we refer to the following papers:
- Matthew Gardner and Yan-Bin Jia. Pose and Motion Estimation of Free-Flying Objects: Aerodynamics, Constrained Filtering, and Graph-Based Feature Tracking. IEEE Transactions on Robotics, vol. 38, no. 5, pp. 3187-3202, 2022.

This material is based upon work supported by the National Science Foundation under Grant IIS-1421034.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Last updated on December 15, 2020.