Robotics Laboratory

Home Members Research Publications Documents Contact

Frictional Impact in 3D

Translation: French

In this page, some formal impulse-based analysis and results on two rigid bodies collision at single contact with Coulomb friction are presented in three dimensions (3D). The model assumes the existence of a virtual spring connecting the two bodies at the contact point, which stores energy when compression first happens during the collision, and then releases the rest of the energy following Stronge's energy-based restitution. The sliding velocity trajectory in the tangential plane, which is called hodograph, yields a non-integrable ordinary differential equation (ODE). Detailed case by case analysis are proposed when the ODE's closed form is available. There are also discussions on faster numerical integration techniques.

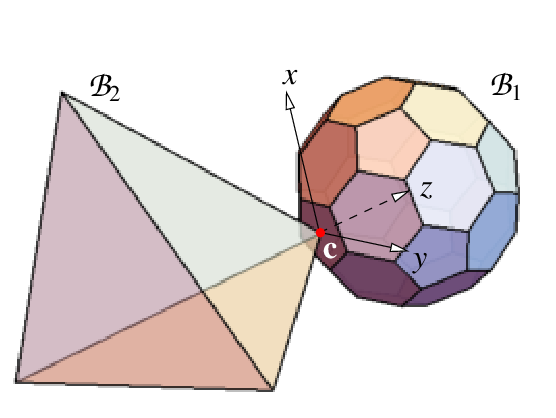
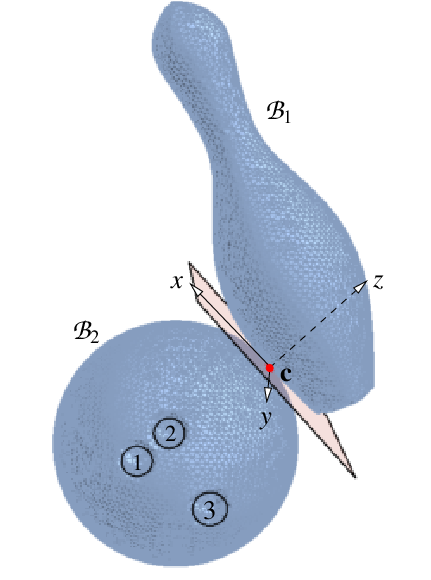
The two figures below show two impact instances. The first figure is a unsymmetric tetrahedron colliding with an icosahedron. The hodographs in the later sessions will all correspond to this instance. Another impact example is between a bowling pin and bowling ball. This instance is used in the fast numerical integration section for comparison. The contact point is denoted as 'C'. Without loss of generality, we set up the normal direction from B₂ to B₁ as 'z'. Then the 'x' and the 'y' directions set up the contact tangential plane.

Invariant Directions and Closed-Form Evaluation

We found that the evolution of the hodograph is always bounded by rays in several invariant directions in the tangential contact plane. Each of the invariant directions can be either a centripetal direction or a centrifugal direction. These invariant directions are determined by the impact configuration and coefficient of friction only, and not by the pre-impact velocities. If the hodograph touches a centripetal invariant direction, it will go towards the origin following the direction. If the hodograph touches a centrifugal invariant direction, it will go away from the origin along the direction. Once the hodograph reaches the origin, it will either terminate or continue in a new centrifugal invariant direction. Some examples of hodographs are presented below:

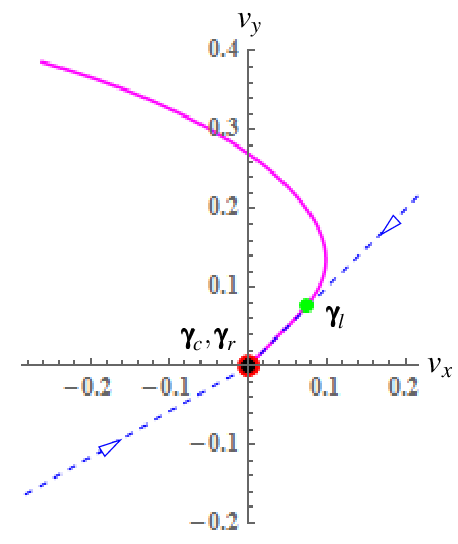
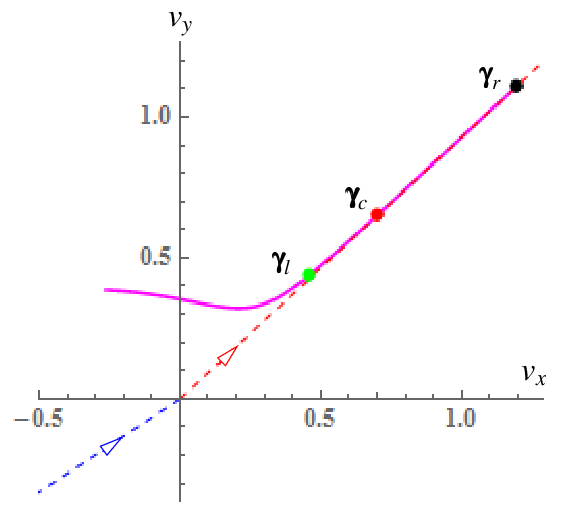
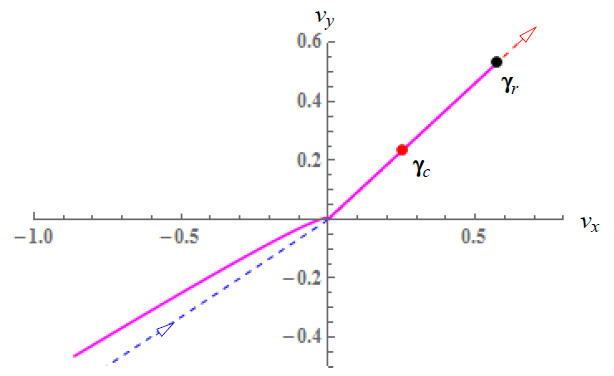
Closed form analysis on the integration of the governing ODE can be applied when the hodograph evolves along any of the invariant direction (event l) or when it turns zero (event s). We denote the end of compression as event c, and the end of restitution as event r. There are eight possible event sequences.

Fast Numerical Integration

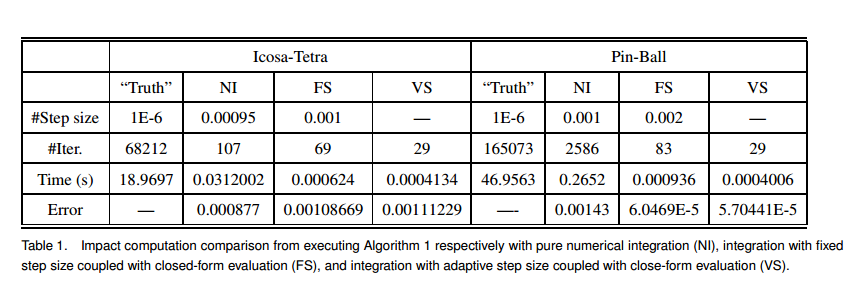
To speed up the numerical integration before closed form analysis can be applied, we use non-uniform stepsizes based on the hodograph curve's speed and curvature. If the hodograph locally curves a lot, which implies that it has a high curvature, then the stepsize is influenced more by the speed--the higher speed the smaller step size. If the curve is locally straight with smaller curvature, then the stepsize is influenced more by the curvature-- the higher curvature the smaller stepsize. Table 1 shows comparisons among different methods when executing the algorithm of computing the outcome of two-body collision in 3D.

Combine fast numerical integration with closed form analysis whenever available, we have a complete algorithm for computing the collision outcome. However, there are still a few more challenges. One challenge is to prove the existence and uniqueness of the impact solution. Another one is about how to predict whether the sliding velocity will reach zero or converge to an invariant direction.

• Yan-Bin Jia, and Feifei Wang. Analysis and computation of two body impact in three dimensions. (422K, 19 pages). ASME Journal of Computational and Nonlinear Dynamics, vol. 12, no. 4, 2017.

---

Last updated on March 29, 2017.