Tangential Compliance in 3-Dimensional Impact
Translations: Indonesian | Russian
Impulse-based manipulation is an area in robotics where very little work is known. An impulsive force has very short execution time, and thus good potential for improving task efficiency. Its use could considerably simplify the robotic mechanism needed to perform a manipulation task, while avoiding uncertainties accumulated over repeated complex operations. The primary reason for the lack of research attention is possibly because the foundation of modeling rigid body impact is not fully developed and the existing theories often seem either too simple to be realistic or too complex to be applicable, especially in the presence of friction and compliance,
We investigate modeling of tangential compliance as two rigid bodies collide in the space. We offer a procedure to compute tangential compliance, and integrate it into impact equations and contact kinematics, making the whole impact system driven by normal impulse alone. Poisson’s hypothesis on restitution, or an energy-based restitution law, is then applied to solve the impact problem.
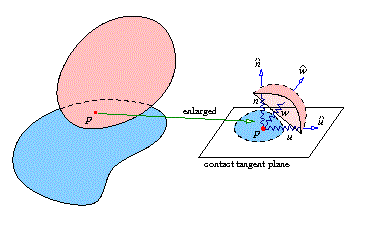We have extended Stronge’s spring-based contact structure to three dimensions. The “contact point” on the upper body does not directly touch the lower body but is rather connected to a massless particle p via three springs respectively aligned with the upward normal and two orthogonal tangential directions, as shown on the left. The velocity of the particle equals the difference between the contact velocity, as determined from contact kinematics, and the composite velocity of the three springs. Slip or stick is indicated by the tangential motion of the particle. Contact modes are eventually described by conditions in terms of the elastic energies stored in these three springs.
We show that the effect of tangential compliance can be analyzed using normal impulse rather than time, contrary to a previous claim by Stronge. This is primarily due to the ability of updating the elastic energies of the three springs without knowledge of their stiffnesses or length changes. The change rates, nevertheless, are computable. So are sliding velocity and tangential impulse.
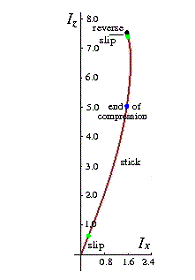
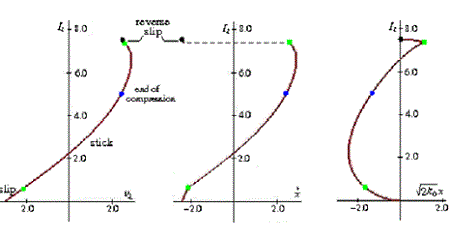
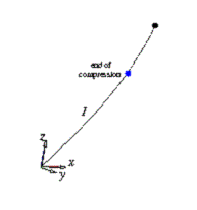
The video on the left below shows repeated bounces of a ball on a table, with initial velocity (-1, 0, -5) and angular velocity (0, 2, 0). The figures to its right show the (planar) impulse curve during the first hit, as well as the evolutions of the contact velocity, the rate of change in length of the tangential spring, and its (scaled) change in length. In each figure, the blue dot indicates the end of restitution, while the green dots indicate contact mode switches. Note the reversal of the ball’s angular velocity after the first bounce.
|
|
|
In the next video, a pencil bounces on the table, resulting in a space impluse curve.
|
|
- Yan-Bin Jia. Energy-based modeling of tangential compliance in 3-dimensional impact. Presented at the Ninth International Workshop on Algorithmic Foundations of Robotics, Singapore, December, 2010.
- Yan-Bin Jia. Three-dimensional impact: energy-based modeling of tangential compliance. (568K, 48 pages). International Journal of Robotics Research, vol. 32, no. 1, pp. 56-83, 2013.
Last updated on Feb 12, 2013.