State Transition Model for Multiple Impacts
Translations: Turkish |
This project started out during Yan-Bin’s 6-month sabbatical visit with Matthew T. Mason and Michael Erdmann at Carnegie Mellon University in 2007, and has since continued primarily at Iowa State University and in China (during breaks). We model a multi-body collision in the impulse space as a state transition diagram, where each state represents a phase during which impacts are “active” at only a subset of the contact points. In the course of the collision, an impact may become active and inactive multiple times, depending on whether the two involved bodies are instantaneously penetrating into each other or not. A state transition happens whenever an active impact finishes restitution, or an inactive impact gets reactivated. The elastic energy due to an impact is not only affected by the impulse at the corresponding contact point, but also by other impulses exerted on the two involved bodies in the duration of this impact. Poisson’s impulse-based law of restitution could result in negative energy. Our new law of restitution governs the loss of elastic energy during the phase. The outcome of a collision depends on the ratios of the contact stiffnesses rather than on their individual values.
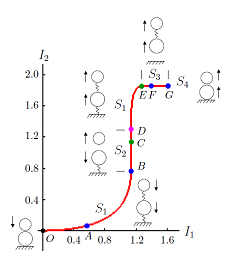
In the representative case of a ball falling onto another on the table (shown to the left below), two impacts, one between the two balls and the other between the lower ball and the table. The curve describing the growth of the two impulses is plotted red in the figure below to the right for a collision instance. The initial configuration is drawn next to the origin with the centers of the two balls vertically aligned. The collision process is described in terms of accumulations of the impulses I1 and I2 at the ball-ball and ball-table contacts, respectively. It is decomposed into a sequence of five states S1 , S2 , S1 , S3 , S4 , which correspond to five segments of growths of (I1 , I2 ): [O, B), [B, D), [D, E), [E, G), and G. In the figure, every state is augmented with a configuration during the state, where active contacts are represented by (virtual) springs.
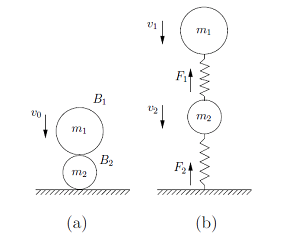
Simultaneous Collisions between Multiple Bodies
The multiple impact model can be integrated with multiple copies of the complient impact model to solve a general simultaneous multibody collision problem. This is done via a decomposition:
- The multiple impact model determines the set of instantaneously active contacts and generates the normal impulses at these contacts based on their differential relationships.
- At every contact, the compliant impact model obtain the tangential impulse from the normal impulse via an energy-based contact mode analysis.
- The normal and tangential impulses are then combined as input to the system dynamics for an update of the velocities of the bodies during the collision.
Modeling Billiard Shots
The collision model is applied to billiard shooting in which the cue stick impacts the cue ball, which in turn impacts the pool table. A billiard with some initial velocity and angular velocity generally slides along a parabolic arc on the pool table and before it starts rolling along a straight trajectory. At the initial stage of this research, we are studying the motion of the cue ball imparted by the cue stick. This motion is a result of simultaneous collisions between the cue stick and the ball, and the ball and the pool table. Up til now, our effort has focused on developing an impact model for simultaneous frictional impacts. The topic has been a subject of controversy in order to be consistent with Coulomb’s law of friction, Poisson’s hypothesis of restitution, and the law of energy conservation.
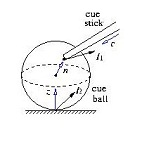
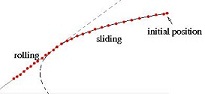
The leftmost figure below illustrates two simultaneous impacts: one between the cue tip and the cue ball and the other between the cue ball and the table. The second figure below plots the positions (dots) of the ball’s center every 1/30th of a second during its motion captured by a camera following a masse shot. Also shown are the trajectory fit over these positions along with the parabola, and the line on which the ball had moved. (Note that the leftmost dot represents only the last position before the ball exited the camera’s field of view.) The third figure below from the left shows the reconstructed trajectory by the integrated impact model — it looks similar to the actual trajectory. The predicted post-shot velocities of the cue ball differ only slightly from those calculated from the video-captured trajectory.
|
|

|
Our long term goal is to design a robot able to play billiards with human-level skills based on understanding of the mechanics. We will integrate work from other areas including vision, control, mechanics, and planning. Existing billiard robot systems focus either on the vision task of recognizing and localizing balls and positioning the cue stick, or on performing simple shots under the guidance of a learning algorithm, a fuzzy expert system, or gray decision theory. To our knowledge, none of the developed systems perform shots based on the mechanics of billiards, or have exhibited preliminary shooting skills.
- Yan-Bin Jia, Matthew T. Mason, and Michael A. Erdmann. A state transition diagram for simultaneous collisions with application in billiard shooting. Presented at the Eighth International Workshop on Algorithmic Foundations of Robotics, Guanajuato, Mexico, December, 2008.
- Yan-Bin Jia, Matthew T. Mason, and Michael A. Erdmann. Multiple impacts: a state transition diagram approach. (672K, 63 pages). International Journal of Robotics Research, vol. 32, no. 1, pp. 84-114, 2013.
Last updated on Feb 12, 2013.