Tactile Shape Recognition Using Differential Invariants
Different from images, tactile data is inherently local but suitable for acquiring during manipulation. The local geometry information it contains suggests the use of differential invariants for recognizing shapes through touch. We are generalizing model-based recognition such that each model in our consideration is a family of parametrized shapes. Our goal is to recover the exact description of a shape from tactile data. Furthermore, we would like to locate the finger(s) on the object where the data were obtained, or equivalently, localizing the object.
In computer vision, a differential invariant is usually independent of certain transformation group but its value depends on the point location on a shape. Multiple invariants of the shape are plotted against each other to define a signature curve so that shape recognition becomes matching corresponding signature curves. This, nevertheless, requires global shape data which are not provided by tactile sensing. With touch sensing we are looking for invariants that are not only independent of the Euclidean transformation but also point locations at which they are evaluated. These shape invariants can be viewed as “indices” for the corresponding shapes.
Low-degree algebraic curves
Ph.D. student Rinat Ibrayev and I are currently looking into 2-D shapes bounded by low-degree polynomial curve segments. We have derived semi-differential invariants for quadratic curves and three special classes of cubic curves. Such an invariant, independent of translation and rotation, is computed from the local geometry at one or more points on the curve. Recognition of a curve class becomes verifying the corresponding invariant with extra data points. The actual curve can be determined in its canonical parametric form using the same tactile data. Finally, the contact locations on the curve are computed, thereby localizing the shape completely relative to the touching hand.
The first figure below shows three ellipses. The second figure shows their signature curves (which plot curvature against its derivative with respect to arc length). Each point in the third figure corresponds to an ellipse with the coordinates equal to its semimajor and semiminor axes. The two axes in the fourth figure represent two invariants and every point corresponds to an ellipse of the same color.
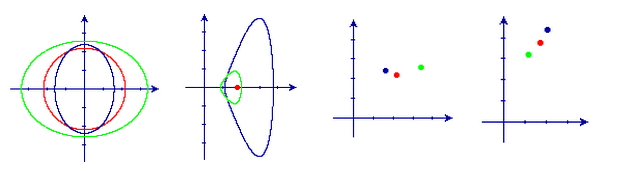
Simulation results support the working of the method in the presence of small noise, although real experiments need to be carried out in the future to demonstrate its applicability. The presented work distinguishes from traditional model-based recognition in its ability to simultaneously recognize as well as localize a shape from one of several classes, each consisting of a continuum of shapes.
Estimation of curvature & derivative
The key for the applicability of our invariant approach lies in obtaining reliable estimates of curvature and its derivative from real data. The tactile data used in our experiments were generated by a joystick sensor mounted on an Adept Cobra 600 robot. Despite the Adept’s high precision, we have found that difference quotients and other numerical methods based on the Taylor expansion are still too sensitive to small measurement errors.
- To estimate curvature, the sensor measures a number of points in its neighborhood. Then we apply quadratic fitting followed by differentiation.
- Obtain curvature estimates at a few points in the neighborhood as above. Approximate arc lengths in between through numerically integrating the respective curve fits. Apply quadratic fitting to these curvatures as a function of arc lengths. Differentiate the resulting curve to obtain the curvature derivative.
The figure on the left below shows 20 points sampled on an elliptic shape by the Adept robot. The second figure plots the pairs of curvature and derivative estimated at these points against the signature curve. The third and fourth figures plot the sample points and their curvature and derivative estimates.
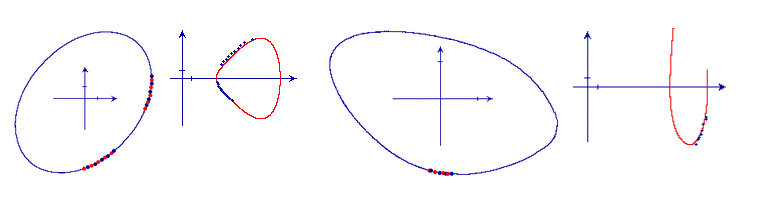
For the elliptic object, the mean estimates on its semimajor and semiminor axes are 2.511269 and 1.719586, which are close to the original values (2.5 and 1.75, respectively).
Recognition tree
We hope to build a recognition tree for subsets of 2D and 3D curved shapes. To recognize a shape, the procedure starts from the root and performs a number of invariant test to reach one classes of shapes (such as ellipses). Then the coefficients of the shape are computed so it is completely determined. Finally, the contact position (indicated by parameter value t) is computed using the same tactile data.
The invariant-based method has the potential of unifying shape recognition, recovery, and pose estimation, all in the domain of touch sensing.
- Rinat Ibrayev and Yan-Bin Jia. Semi-Differential Invariants for Tactile Recognition of Algebraic Curves. International Journal of Robotics Research, vol. 24, no. 11, pp. 951-969, 2005.
- Rinat Ibrayev and Yan-Bin Jia. Tactile recognition of algebraic shapes using differential invariants. Proceedings of the IEEE International Conference on Robotics and Automation, pp. 1548-1553, New Orleans, LA, Apr 26-May 1, 2004.
 This material is based upon work supported by an NSF CAREER Award 0133681.
This material is based upon work supported by an NSF CAREER Award 0133681.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Last updated on Sep 14, 2006.